|
Bank Angle and the Physics of Standard Rate Turns (continued)
IX - Other Useful Information that We Can Use From Our Study
As we constructed our mathematical model for standard rate turns we came across many formulas that are useful. In this section lets quickly highlight a few.
A - Radius of Turn Formula (as a function of speed and rate of turn)
where r is the radius of turn, v is the speed of the aircraft and 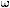 is the rate of turn. Variables r, v and is the rate of turn. Variables r, v and 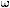 are in SI units: m, m/s and rad/s. We will apply the conversion multipliers so that r, v,and are in SI units: m, m/s and rad/s. We will apply the conversion multipliers so that r, v,and 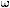 can be given in Nm, knots and o/s respectively. Applying the conversion multipliers on table 8-3: can be given in Nm, knots and o/s respectively. Applying the conversion multipliers on table 8-3:
Renaming r, v and 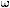 to the more user friendly RadiusOfTurn, TAS (true airspeed) and RateOfTurn respectively, we have: to the more user friendly RadiusOfTurn, TAS (true airspeed) and RateOfTurn respectively, we have:
where RadiusOfTurn, TAS and RateOfTurn are given in Nm, knots and o/s respectively.
Evaluating 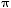 and fractions to five significant digits: and fractions to five significant digits:
For a standard rate turn (RateOfTurn = 3o/s) ONLY, we have:
RadiusOfTurn = 0.00053052 · TAS
where RadiusOfTurn and TAS are given in Nm and knots respectively. This equation is exact up to five significant digits.
B - Radius of Turn Formula (as a function of speed and bank angle)
Equation 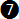 can be rearranged and solved for "r" as follows: can be rearranged and solved for "r" as follows:
where r is the radius of turn, v is the speed of the aircraft, g is the acceleration of gravity and 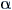 is the angle of bank. Variables r, v, g and is the angle of bank. Variables r, v, g and 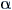 are in SI units: m, m/s, m/s2 and rad respectively. We are going to keep "g" in SI units and use the standard value of 9.80665 m/s2 for it. We will apply the conversion multipliers so that r, v,and are in SI units: m, m/s, m/s2 and rad respectively. We are going to keep "g" in SI units and use the standard value of 9.80665 m/s2 for it. We will apply the conversion multipliers so that r, v,and 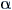 can be given in Nm, knots and o respectively. Applying the conversion multipliers on table 8-3: can be given in Nm, knots and o respectively. Applying the conversion multipliers on table 8-3:
Renaming r, v and 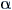 to the more user friendly RadiusOfTurn, TAS (true airspeed) and BankAngle, we have: to the more user friendly RadiusOfTurn, TAS (true airspeed) and BankAngle, we have:
where RadiusOfTurn, TAS and BankAngle are given in Nm, knots and o respectively.
Evaluating 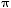 and fractions to five significant digits: and fractions to five significant digits:
C - Load Factor Formula (as a function of bank angle)
Load factor is defined as the total lift to weight ratio:
| |
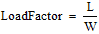 |
 |
(new equation) |
Where L is the total lift and W is the weight of the aircraft. We now need to find an equation for L:
From our triangle that we got from analyzing the geometry of a standard rate turn in section III we can get the following equation that will give us total lift (L):
Where 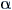 , LV, and L are the bank angle, vertical lift and total lift respectively. Since vertical lift has to equal weight: , LV, and L are the bank angle, vertical lift and total lift respectively. Since vertical lift has to equal weight:
we can substitute  in in 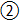 to get: to get:
we can substitute  in in  to get: to get:
Notice how weight (W) cancelled out. Note that 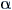 is in SI unit: radians. LoadFactor has no unit. We will apply the conversion multiplier so that is in SI unit: radians. LoadFactor has no unit. We will apply the conversion multiplier so that 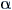 can be given in o. Applying the conversion multiplier on table 8-3: can be given in o. Applying the conversion multiplier on table 8-3:
| |
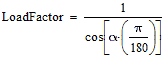 |
 b b |
|
Renaming  to the more user friendly BankAngle, we have: to the more user friendly BankAngle, we have:
| |
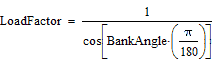 |
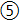 c c |
|
Evaluating 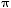 and fractions to five significant digits: and fractions to five significant digits:
| |
 |
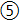 d d |
|
where BankAngle is given in o. The charts below graph this formula.
| |
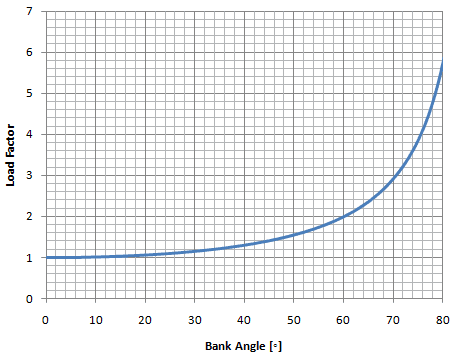
Load Factor vs Bank Angle (at bank angles up to 80o)
 |
|
Chart 9-1
Chart 9-1 graphs the load factor at bank angle up to 80o. At 80o the load factor is almost 6. This would mean that a pilot performing a level turn at this bank angle would experience almost 6 times the force of gravity (or 6g's).
| |
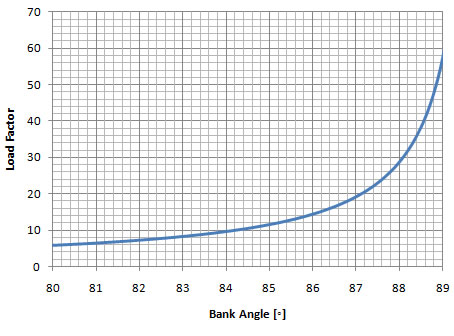
Load Factor vs Bank Angle (at bank angles from 80o to 89o)
 |
|
Chart 9-2
Chart 9-2 graphs the load factor at bank angles from 80o to 89o. Notice how abruptly the load factor increases. As the bank angle approaches 90o, the load factor approaches infinity (not possible to show in the graph).
|

