|
Bank Angle and the Physics of Standard Rate Turns (continued)
IV - Obtaining Approximate Equations for Mentally Estimating the
Bank Angle Required for Standard Rate Turn
Arctangent Approximation
Under certain conditions:
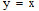
is a very good approximation of:
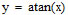
Note that the atan (arctangent) function must be in radians.
Comparing Numerical Values for Arctangent
(in Radians) with the Approximation |
| |
| x |
0.000 |
0.087 |
0.176 |
0.268 |
0.364 |
0.466 |
0.577 |
0.700 |
| y = atan (x) |
0.000 |
0.087 |
0.174 |
0.262 |
0.349 |
0.436 |
0.523 |
0.611 |
| y = x |
0.000 |
0.087 |
0.176 |
0.268 |
0.364 |
0.466 |
0.577 |
0.700 |
| Error (difference) |
0.000 |
0.000 |
0.002 |
0.006 |
0.015 |
0.030 |
0.054 |
0.089 |
| Error % |
0% |
0% |
1% |
2% |
4% |
7% |
10% |
15% |
| |
|
|
Table 4-1
Table 4-1 above shows several values for x and the corresponding y results. Decimals were placed to indicate the precision that the calculations were made. Notice that for values under 0.268 the difference is 2% or less.
| |
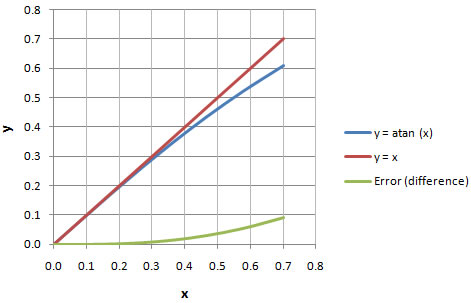
Arctangent (in Radians) Approximation and Error
 |
|
Chart 4-1
In chart 4-1 you can visualize how the y = atan (x) function is very close to the straight line given by y = x for values closer to zero.
It is hard to see what this means for us when we are working in radians. The arctangent (atan) function in radians can be converted to degrees by simply multiplying it by a conversion constant c1.
Therefore we have:
| |
 |
where: |
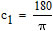 |
and the simplified function will be:
| |
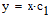 |
where: |
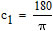 |
Comparing Numerical Values for Arctangent
(in Degrees) with the Approximation |
| |
| x |
0.000 |
0.087 |
0.176 |
0.268 |
0.364 |
0.466 |
0.577 |
0.700 |
| y = atan (x) · c1 |
0.0 |
5.0 |
10.0 |
15.0 |
20.0 |
25.0 |
30.0 |
35.0 |
| y = x · c1 |
0.0 |
5.0 |
10.1 |
15.4 |
20.9 |
26.7 |
33.1 |
40.1 |
| Error (difference) |
0.0 |
0.0 |
0.1 |
0.4 |
0.9 |
1.7 |
3.1 |
5.1 |
| Error % |
0% |
0% |
1% |
2% |
4% |
7% |
10% |
15% |
| |
|
|
Table 4-2
Table 4-2 shows the values of y in degrees. For example when the value of the arctangent in degrees is 20, the simplified function will have a value of 20.9. This difference of 0.9 is approximately a 4% error. The higher the amount of degrees, the higher the error. For 35o the error is 15%. However for smaller angles the error is practically negligible.
| |
Arctangent (in Degrees) Approximation and Error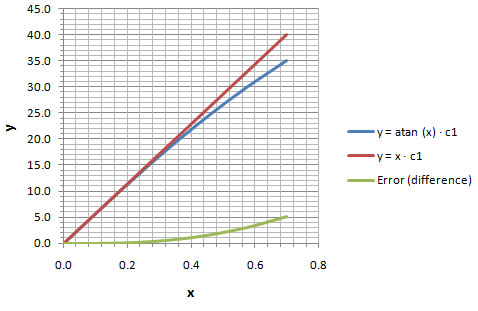 |
|
Chart 4-2
Chart 4-2 helps visualize how the error is very minute for small angles and gets progressively larger once you pass about 25o.
Applying the Arctangent Approximation to our Formula for Bank Angle
Bank Angle = 57.296 · atan (0.0027467 · TAS)  c c
Applying our simplification for arctangent, equation  c becomes: c becomes:
Bank Angle 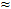 57.296 · 0.0027467 · TAS 57.296 · 0.0027467 · TAS
Once again "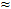 " is just a reminder that this is an approximation. Now if we multiply the two numbers in our equation we will have: " is just a reminder that this is an approximation. Now if we multiply the two numbers in our equation we will have:
Bank Angle 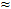 0.15737 · TAS 0.15737 · TAS 
Notice how remarkably close equation  is to the rule of thumb formula discussed in the beginning of this article: is to the rule of thumb formula discussed in the beginning of this article:
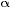 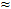 0.15 · TAS 0.15 · TAS
or:
Bank Angle 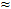 0.15 · TAS 0.15 · TAS
We had to go a long ways, but now we know where the rule of thumb formula comes from and what modifications had to be done to the exact formula in order to obtain it. Remember that Bank Angle in these two formulas is in degrees and TAS is in knots.
In summary we have the following (see table 4-3 below) equations for obtaining the bank angle for standard rate turn as a function of true airspeed (TAS):
| Bank Angle Equations for Standard Rate Turn |
| |
| Equation Number |
Equation |
Exact |
 c c |
Bank Angle = 57.296 · atan (0.0027467 · TAS) |
yes* |
 |
Bank Angle 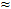 0.15737 · TAS 0.15737 · TAS |
no |
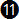 |
Bank Angle 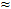 0.15 · TAS 0.15 · TAS |
no |
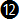 |
Bank Angle 0.10 · TAS + 5 0.10 · TAS + 5 |
no |
| * Up to 5 significant digits |
 |
|
|
Table 4-3
The two rule of thumb equations that we discussed in the beginning of the article were numbered 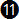 and and 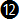 so that we can refer to them later in the text. These are the equations that are easily mentally calculated because of their simplicity. In the next section we'll examine how precise they are. so that we can refer to them later in the text. These are the equations that are easily mentally calculated because of their simplicity. In the next section we'll examine how precise they are.
|

