| Mentally Calculating the Wind Correction Angle by Luiz Roberto Monteiro de Oliveira © 2010 Luiz Roberto Monteiro de Oliveira |
I - Introduction
A skill that gives a huge advantage to the instrument pilot, is the ability to mentally estimate, in flight, the wind correction angle (WCA) also known as crab angle. The following section will show you how to do this.
 |
|
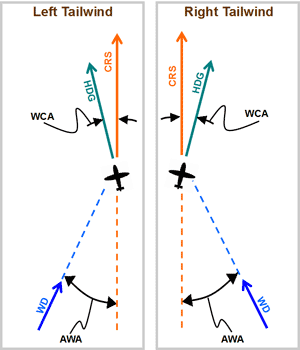 |
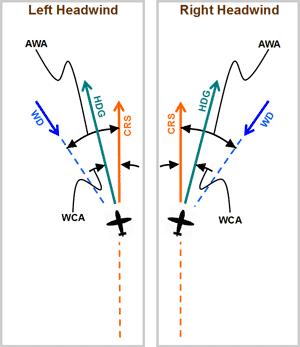
Fig 1 Visualizing the wind correction angle (WCA)
Fig 1 - ABBREVIATIONS: CRS*: course |
Fig 1 - TERMS: acute angle: an angle less than 90o |
The wind correction angle (WCA) is the angle between the course (CRS) and the heading (HDG) that is required for the aircraft to track that course when there is wind (see figure 1). The WCA is basically added (when the wind is to the right) or subtracted (when the wind is to the left) to the course. The result of this addition or subtraction is the heading which the pilot must fly to maintain that course.
On figure 1, note the following:
- The wind correction angle (WCA) is always on the same side of the CRS line as the wind direction (WD).
- The heading (HDG) to track the course (CRS) will always lie somewhere between the CRS and the wind direction (WD).
| * | When calculating the WCA for a desired track (TRK) simply substitute TRK in place of course (CRS) and use the method outlined in this article. The formula for heading then would be as follows. | |
II - Method for estimating the wind correction angle (WCA)
Step 1: Most aircraft have a typical cruising speed. Determine what is the most common true airspeed that you fly at.
Step 2: Determine your maximum wind correction angle (WCAmax), for a wind speed (WS) of 10 knots, using the formula below at the true airspeed (TAS) that you just obtained above (step 1). This will be the WCA when the wind direction (WD) is 90o in relation to the CRS line. The exact maximum wind correction angle is given by:
where WS is the wind speed, and TAS is the aircraft's true airspeed. Make sure your calculator is in DEG (degrees) mode. In this example the WS is 10 knots and the TAS is 110 knots. Therefore we will have:
which means that in the worst case scenario when the wind is 90o in relation to our desired course (same as AWA=90o), the wind correction angle (WCA) is 5o for a wind of 10 knots at our true airspeed of 110 knots. You should memorize this result of 5o for your WCAmax.
Step 3: Remember a few simple rules:
- If the wind speed doubles, triples, etc., your wind correction angle (WCA) will be approximately double, triple, etc. respectively. This works for wind speeds up to 50% of true airspeed (TAS).
- If the wind speed decreases in half, a third, etc., your correction angle (WCA) will be approximately half, one third, etc. respectively.
- If your aircraft's true airspeed (TAS) doubles, triples, etc. the wind correction will be approximately half, one third, etc. respectively of what it was.
- if your aircraft's true airspeed (TAS) is halved, is one third, etc., the wind correction will be approximately double, triple, etc. respectively of what it was.
The reason we used 10 knots for wind speed (WS) when we calculated WCAmax is that it is an easy number to work with later when we have other wind speeds. For example if the wind speed is 20 knots we know easily that 20 knots is two times more than 10 knots, therefore the wind correction angle will be double.
Step 4: The correction factor is based on the acute wind angle (AWA). This is one of the two angles, whichever one is 90o or less, formed by the wind direction and the CRS line. Memorize the correction factors for the WCA when the wind is from directions other than 90o in relation to our course (AWA not equal to 90o). The following table lists these correction factors. Remember that you are just getting a really rough number so that you can estimate your initial WCA (crab angle) when intercepting or tracking a course.
|
or |
|
||||||||||||||||||||||||||||||||
| (a) | (b) |
Fig 2 Correction factors for maximum wind correction angle
There are two tables above, the first one (left) is more complete and more precise. We will use the less precise table on the right for our examples. You will see that even with this more simplified table we will get a pretty good estimate.
To figure out your wind correction angle (WCA) just multiply the maximum wind correction angle by the appropriate factor. If wind speed is the same** as the one used to calculate WCAmax***, we have:
| ** | Later in the text we will also discuss how to adjust when the wind speed is other than the 10 knots we used for our WCAmax. We will be applying the rules in step 3. I'll also show you how to visualize the AWA using your aircraft instruments. |
| *** | Note: the dot (.) in the formula above means multiply. |
In the table, use the AWA that is closest to the value that you have. For example: for an AWA of 33o use the 30o correction factor which is 1/2 or 0.5 (see figure 2b). If you calculated WCAmax to be 5o, your WCA will be 5o x 0.5 or 5/2 = 2.5o. Round that to the nearest degree and get 3o for your estimated correction angle.
You can compare your estimated wind correction angle (WCA) with the formula below (this formula is exact) to determine how far you are off. Remember that your goal using the technique above is just to get a rough idea of what the wind correction angle is, it does not have to be exact.
III - Applying the method
Example:
If your typical cruising true airspeed is 130 kts for your aircraft. Estimate the wind correction angle (WCA) for the following conditions:
a) WS = 10 knots; AWA = 40o
b) WS = 20 knots; AWA = 40o
c) WS = 5 knots; AWA = 40o
d) WS = 10 knots; AWA = 70o
e) WS = 30 knots; AWA = 90o
f) WS = 20 knots; AWA = 10o
g) WS = 27 knots; AWA = 60o
h) WS = 3 knots; AWA = 45o
i) WS = 12 knots; AWA = 20o
j) WS = 48 knots; AWA = 70o
k) WS = 63 knots; AWA = 25o
Solution:
| Step 1: We know the typical cruising speed is 130 kts TAS. |
|||
| Step 2: Calculate the maximum wind correction angle using the formula below for a wind speed (WS) of 10 knots:
substituting 130 knots for TAS and 10 knots for WS we have: This maximum correction angle result (WCAmax) of 4o will be the basis for all our estimates of wind correction angles (WCA) when the aircraft's true airspeed is around 130 knots. |
Estimating each part using the mental calculation method:
a) WS = 10 knots; AWA = 40o
| Step 3: Since the WS of 10 knots is the same as the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be the same: 4o. |
|
| Step 4: Next we look at the table in figure 2b and see what value is closest to 40o. If we use the table on the right, 40o is right in the middle between 30o and 50o. If it's in the middle, choose the value for the next highest one which will be for 50o. The factor is 3/4 or 0.75. Therefore our estimated wind correction will be 4o x 0.75 = 3o. |
b) WS = 20 knots; AWA = 40o
| Step 3: Since the WS of 20 knots is double the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be doubled: 4o x 2 = 8o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 40o. If we use the table on the right, 40o is right in the middle between 30o and 50o. If it's in the middle, choose the value for the next highest one which will be for 50o. The factor is 3/4 or 0.75. Therefore our estimated wind correction will be 8o x 0.75 = 6o. |
c) WS = 5 knots; AWA = 40o
| Step 3: Since the WS of 5 knots is half of the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be halved: 4o / 2 = 2o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 40o. If we use the table on the right, 40o is right in the middle between 30o and 50o. If it's in the middle, choose the value for the next highest one which will be for 50o. The factor is 3/4 or 0.75. Therefore our estimated wind correction will be 2o x 0.75 = 1.5o. You can round that up to 2o. |
d) WS = 10 knots; AWA = 70o
| Step 3: Since the WS of 10 knots is the same as the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be the same: 4o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 70o. If we use the table on the right, 70o is going to be a factor of 1. Therefore our estimated wind correction will be 4o x 1 = 4o. |
e) WS = 30 knots; AWA = 90o
| Step 3: Since the WS of 30 knots is three times the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be tripled: 4o x 3 = 12o. |
|
| Step 4: Since the wind direction is 90o in relation to our course the wind correction angle will be the maximum. Therefore WCA = 12o. |
f) WS = 20 knots; AWA = 10o
| Step 3: Since the WS of 20 knots is double the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be doubled: 4o x 2 = 8o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 10o. In this case it will be for 0o. The factor is 0. Therefore our estimated wind correction will be 0o. |
g) WS = 27 knots; AWA = 63o
| Step 3: Round the WS to the nearest multiple of 5, so for a WS of 27 knots, we will calculate as if the WS was 25 knots. Since the WS of 25 knots is 2.5 or 2 1/2 times the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be 2 1/2 times that: 4o x (2 + 1/2) = 8o + 2o = 10o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 63o. If we use the table on the right, 60o is going to be a factor of 1. Therefore our estimated wind correction will be 10o x 1 = 10o. |
h) WS = 3 knots; AWA = 45
| Step 3: For wind speed less the 5 knots I would probably just ignore them and assume the WCA is 0o. However, we were to use this method, round the WS to the nearest multiple of 5, so for a WS of 3 knots, we will calculate as if the WS was 5 knots. Since the WS of 5 knots is half of the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be halved: 4o / 2 = 2o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 45o. If we use the table on the right, 50o is going to be a factor of 3/4 or 0.75. Therefore our estimated wind correction will be 2o x 0.75 = 1.5o. You can round that up to 2o. |
i) WS = 12 knots; AWA = 20o
| Step 3: Round the WS to the nearest multiple of 5, so for a WS of 12 knots, we will calculate as if the WS was 10 knots. Since the WS of 10 knots is the same as the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be the same: 4o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 20o. If we use the table on the right, 30o is going to be a factor of 1/2 or 0.5. Therefore our estimated wind correction will be 4o x 1/2 = 2o. |
j) WS = 48 knots; AWA = 70o
| Step 3: Round the WS to the nearest multiple of 5, so for a WS of 48 knots, we will calculate as if the WS was 50 knots. Since the WS of 50 knots is five times the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be five times greater: 4o x 5 = 20o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 70o. If we use the table on the right, 60o is going to be a factor of 1. Therefore our estimated wind correction will be 20o x 1 = 20o. |
k) WS = 63 knots; AWA = 25o
| Step 3: Round the WS to the nearest multiple of 5, so for a WS of 63 knots, we will calculate as if the WS was 65 knots. Since the WS of 65 knots is 6 and 1/2 times the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be 6 and 1/2 more: 4o x (6 + 1/2)= 24o+2o = 26o. |
|
| Step 4: Next we look at the table on figure 2b and see what value is closest to 25o. If we use the table on the right, 30o is going to be a factor of 1/2 or 0.5. Therefore our estimated wind correction will be 26o x 1/2 = 13o. |
IV - Comparing the mental estimation method with the exact formula
Although using the exact formula for calculating WCA would defeat the purpose of doing the mental estimation, we can use it here to compare and see how close our estimations were. The following formula produces an exact result:
a) WS = 10 knots; AWA = 40o.
Substituting the values in the equation:
The WCA calculated by the formula is 3o. This is the same result we got using mental estimation.
b) WS = 20 knots; AWA = 40o.
The WCA calculated by the formula is 6o. This is the same result we got using mental estimation.
c) WS = 5 knots; AWA = 40o.
Substituting the values in the equation:
The WCA calculated by the formula is 1o. This result we got using mental estimation was 2o so we are off by 1o.
d) WS = 10 knots; AWA = 70o
Substituting the values in the equation:
The WCA calculated by the formula is 4o. This is the same result we got using mental estimation.
e) WS = 30 knots; AWA = 90o.
Substituting the values in the equation:
The WCA calculated by the formula is 13o. This result we got using mental estimation was 12o so we are off by 1o.
f) WS = 20 knots; AWA = 10o
Substituting the values in the equation:
The WCA calculated by the formula is 0o. This result we got using mental estimation was 2o so we are off by 2o.
g) WS = 27 knots; AWA = 63o.
Substituting the values in the equation:
The WCA calculated by the formula is 11o. This result we got using mental estimation was 10o so we are off by 1o.
h) WS = 3 knots; AWA = 45o
Substituting the values in the equation:
The WCA calculated by the formula is 1o. This result we got using mental estimation was 2o so we are off by 1o.
i) 12 knots; AWA = 20o
Substituting the values in the equation:
The WCA calculated by the formula is 2o. This is the same result we got using mental estimation.
j) WS = 48 knots; AWA = 70o
Substituting the values in the equation:
The WCA calculated by the formula is 20o. This is the same result we got using mental estimation.
k) WS = 63 knots; AWA = 25o
Substituting the values in the equation:
The WCA calculated by the formula is 12o. This result we got using mental estimation was 13o so we are off by 1o.
Notice how close our estimates were, even using the simpler table on the right for the AWA correction!
V - Techniques for visualization of wind during flight
During flight the pilot will need to visualize where the wind is in relation to the aircraft's heading and course. The following are a few suggestions on how to do this and figure out what the AWA is.
Heading bug
| (a) | (b) | (c) |
Fig 3 Heading bug on heading indicator (a), analog HSI (b) and digital HSI (c).
If the heading bug (figure 3) is not being used by the autopilot, or for other reasons, the heading bug can be set to remind the pilot where the wind is.
Visualizing the AWA before intercepting the course (CRS)
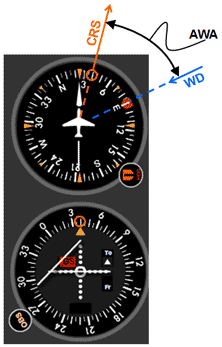 |
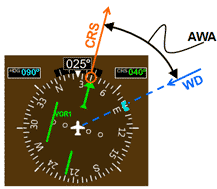
Fig 4 Visualizing the AWA using the heading indicator for a right head wind.
Figure 4 illustrates how a heading bug can be used on a heading indicator to remind the pilot where the wind is coming from. In this case the wind direction (WD) is from 090. If the course (CRS) that is going to be navigated is 040, for example, the pilot can visualize the 040 mark on the heading indicator to be that course. In this case wind is coming from the front (headwind), therefore the angle between the course (CRS) and the wind (WD) will be the acute wind angle (AWA). If the wind were a tail wind the AWA would be the angle between the reciprocal of the course (CRS+180) and the wind direction (WD).
Knowing the AWA allows you to calculate, using the techniques described in the previous paragraphs, the wind correction angle (WCA). Once the pilot has intercepted the course (CRS), the WCA can be added or subtracted from the CRS to determine the heading (HDG) that is required to maintain that course and compensate for the wind. In this particular example since the CRS is 040 and WD is 090, the AWA is 90-40 = 50o.
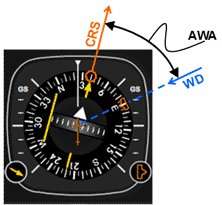 |
 |
|||
| (a) | (b) |
Fig 5 Visualizing the AWA using an analog (a) and digital (b) HSI for a right head wind.
Figure 5 shows how to visualize the above scenario's AWA on an analog and digital HSI. If for some reason the heading bug is being used for something else the pilot can make a mental note of where the wind is instead. Having a general idea of the wind is crucial to smooth and accurate navigation.
If the wind speed (WS) in this example is 40 knots and the aircraft's true airspeed (TAS) is at 110 knots. Calculate the wind correction angle (WCA).
First let's summarize the information we have and don't have:
CRS = 040
WD = 090
WS = 40 knots
AWA = 50o
TAS =
110 knots
WCAmax for a 10 knot wind= ?
WCA=?
To use our method of mentally calculating the wind correction angle (WCA) we have to first calculate and memorize the maximum wind correction (WCAmax) for a 10 knot wind at our typical true airspeed (TAS) of 110 knots.
The maximum wind correction angle is given by:
where WS is the wind speed, and TAS is the aircraft's true airspeed. Make sure your calculator is in DEG (degrees) mode. In the case even though the actual WS is 40 knots, we will use 10 knots to calculate our base (WCAmax) . Remember that we will only have to do this once, and then it will serve as the basis for any calculation of the WCA for our typical true airspeed.
This means that in the worst case scenario for a 10 knot wind when the wind direction is 90o in relation to our desired course, the wind correction angle (WCA) is 5o. Therefore WCAmax for a 10 knot wind = 5o.
Lets now calculate WCA given: WS = 40 knots; AWA = 50o. Begin by rounding the WS to the nearest multiple of 5, so for a WS of 40 knots, we already have it as a multiple of 5. Since the WS of 40 knots is four times the 10 knots we used to calculate the maximum wind correction angle (WCAmax), our maximum wind correction angle for this wind speed is going to be quadrupled: 5o x 4 = 20o. Next we look at the table on figure 2(b) and see what value is closest to 50o. If we use the table on the right, 50o is going to be a factor of 3/4 or 0.75. Therefore our estimated wind correction: WCA = 20o x 3/4 = 15o.
Visualizing the wind correction angle (WCA) once established on the course (CRS)
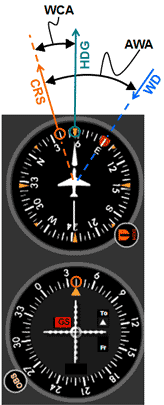 |
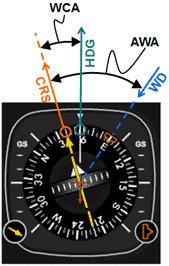
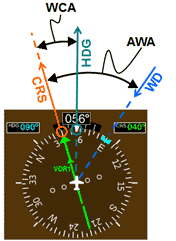
Fig 6 Visualizing the WCA once established on course (CRS).
The VOR instrument needle is centered once on course (figure 6). If at this point the aircraft is on the correct heading to maintain course (keep the needle centered), the difference between the course and this heading will be the wind correction angle (WCA). In practice, the pilot that has mentally calculated the wind correction angle will be able to estimate what this heading is by adding or subtracting the WCA to the CRS. In this case the wind is to the right of the course so the WCA will be added to CRS to get the heading (HDG). Specifically in the example above, the CRS is 040 and the mentally calculated WCA is 15o, therefore: HDG = 040 + 15o = 055.
Previously when intercepting the 040 course the pilot will maneuver in such a way that the aircraft will be at the 055 heading when the needle of the VOR instrument is centered. Once on course the pilot may have to make minor adjustments to the aircraft's heading in order to keep the needle centered. This is to correct for the actual wind which may be different than the forecast wind, or for an error in the mental calculation of the WCA. In this example, the exact WCA turns out to be 16o. This 1odifference is the minor adjustment that the pilot had to make. Therefore the pilot is now flying at a HDG of: 040 + 16o = 056.
 |
 |
|||
| (a) | (b) |
Fig 7 Visualizing the WVA and AWA using an analog (a) and digital (b) HSI.
Figure 7 shows how to visualize the above scenario's WCA and AWA on an analog and digital HSI.
Other examples for winds from other directions
Below are a few other examples of how to visualize wind correction angle (WCA) and acute wind angle to course line (AWA), for winds that are coming from other directions. The examples deliberately have the same AWA of 50o so that we can use the same WCA of 16o which was already calculated.
Example 2
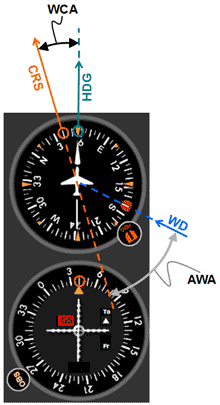 |
Fig 8 Visualizing a right tail wind using a VOR instrument and the heading indicator.
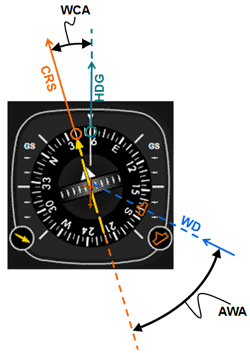 |
 |
|||
| (a) | (b) |
Fig 9 Visualizing a right tail wind using an analog (a) and digital (b) HSI instrument.
In figures 8 and 9 we have the following configuration:
CRS = 040
WD = 170 (right tail wind)
Reciprocal course (CRS + 180) = 220
AWA = 50o
WCA = 16o
HDG = 040 + 16o = 056
Example 3
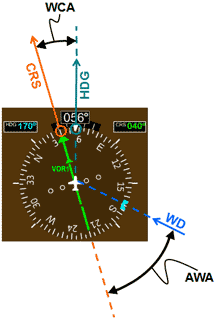
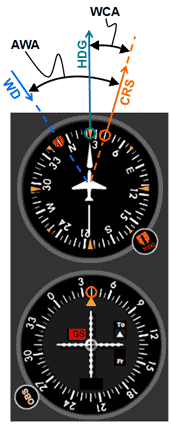 |
Fig 10 Visualizing a left head wind using a VOR instrument and the heading indicator.
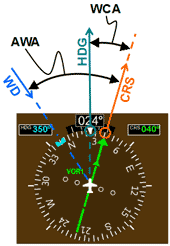 |
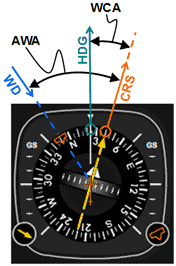 |
|||
| (a) | (b) |
Fig 11 Visualizing a left head wind using an analog (a) and digital (b) HSI instrument.
In figures 10 and 11 we have the following configuration:
CRS = 040
WD = 350 (left head wind)
AWA = 50o
WCA = 16o
HDG = 040 - 16o = 024
Example 4
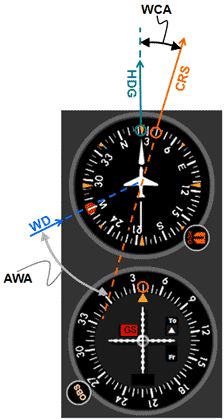 |
Fig 12 Visualizing a left tail wind using a VOR instrument and the heading indicator.
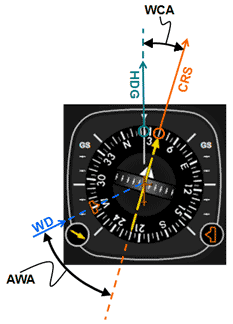 |
 |
|||
| (a) | (b) |
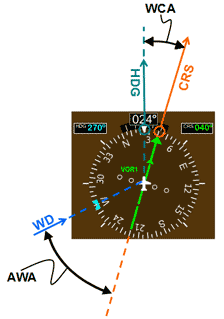
Fig 13 Visualizing a left tail wind using an analog (a) and digital (b) HSI instrument
In figures 12 and 13 we have the following configuration:
CRS = 040
WD = 270 (left tail wind)
AWA = 50o
WCA = 16o
HDG = 040 - 16o = 024
All rights reserved to Luiz Roberto Monteiro de Oliveira.